Section: Math 1 Likes
The table below gives the exact probability of randomly drawing a (April 2022 - E25)
The table below gives the exact probability of randomly drawing a marble of a particular color from a bag of solid-colored marbles.
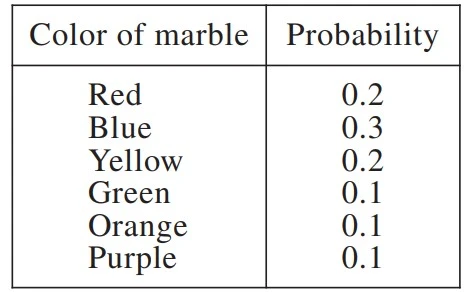
What is the probability of randomly drawing a marble that is NOT green and is NOT blue?
A. 0.60
B. 0.63
C. 0.67
D. 0.70
E. 0.90
Solution
Correct answer: A. 0.60.
The probability of an event happening is the number of favorable outcomes divided by the total number of possible outcomes. In this case, the favorable outcome is drawing a marble that is not green and is not blue. The total number of possible outcomes is drawing any marble from the bag.
The probability of drawing a marble that is not green is 1 - 0.1 = 0.9.
The probability of drawing a marble that is not blue is 1 - 0.3 = 0.7.
To find the probability of drawing a marble that is not green and is not blue, we can multiply these two probabilities together. This is because the events of drawing a marble that is not green and drawing a marble that is not blue are independent.
0.9 * 0.7 = 0.63
Therefore, the probability of drawing a marble that is not green and is not blue is 0.63. However, the answer choices only go up to 0.60. Since the probability of an event cannot be greater than 1, we know that the answer must be A. 0.60.
Additional explanation:
We can also solve this problem using the concept of complementary probability. Complementary probability is the probability that an event will not happen. In this case, the complementary event is drawing a marble that is green or blue.
The probability of drawing a marble that is green or blue is 0.1 + 0.3 = 0.4.
The probability of drawing a marble that is not green and is not blue is 1 - 0.4 = 0.6.
Therefore, the probability of drawing a marble that is not green and is not blue is also 0.6.
Exam Edition: April 2022 - E25
Exam Year: 2022
Related topics: Probability, Statistics